W poprzednim odcinku otrzymaliśmy całkiem przyzwoity generator liczb o rozkładzie równomiernym. Teraz uzupełnimy naszą klasę o metodę do pobierania wartości z rozkładu normalnego, zwanego też rozkładem Gaussa.

Zastosowanym algorytmem do generowania liczb losowych z rozkładu normalnego jest implementacja metody Kindermana i Monahana, zwanej ROU (ratio-of-uniforms method). Szczegóły tej metody można znaleźć w książce Wieczorkowskiego i Zielińskiego[2]

Moja implementacja w języku C++ zawarta jest w metodzie getFromNormalDistribution() klasy RandomNumberGenerator i wygląda następująco:

double RandomNumberGenerator::getFromNormalDistribution() {

    bool ok = false;
    double limit = sqrt(2/2.718281828);
    double X;

    do {
        // generuj U o rozkładzie równomiernym U(0,1)
        double U = getFromUniformDistribution();

        // generuj V o rozkładzie równomiernym
        // U(-sqrt(2/e),sqrt(2/e))

        double V = 2 * limit * getFromUniformDistribution() - limit;
        X = V / U;

        if (X*X <= 2*(3-U*(4+U))) {

            ok = true;

        } else if (X*X <= 2/U - 2*U) {

            if (X*X <= -4*log(U)) {
               ok = true;
            }

        }
    } while (!ok);

    return X;
}

Jak widać używa on metody getFromUniformDistribution() zdefiniowanej wcześniej a zwracającej nam dwie liczby z rozkładu równomiernego, jedna z przedziału (0,1) a druga z (-sqrt(2/e), sqrt(2/e)).

Ok. Teraz wypadałoby jakoś przetestować nasz generator. Do tego celu napiszemy szybko programik generujący histogram otrzymywanych wartości. Oto on:

#include <iostream>
#include <vector>
#include <math.h>
#include "source/RandomNumberGenerator.cpp"

using namespace std;

int main(int argc, char* args[]) {

    // wektor przechowywujący liczebność wylosowanych liczb w danym przedziale
    vector<double> histogram;

    double min = -3;   // dolna granica
    double max = 3;    // górna granica
    double n = 1000;   // liczba przedziałów

    // krok o jaki będą zwiększać się kolejne przedziały
    double step = (max - min) / n;

    // zainicjowanie licznikow
    for (int i = 0; i < n; i++) {
       histogram.push_back(0);
    }

    // losowanie i określenie w którym przedziale znajduje się wylosowana liczba
    for (int k = 0; k < 10000000; k++) {

        // pobranie wartości losowej
        double X = RandomNumberGenerator::Instance()->getFromUniformDistribution();

        // 'odległość' od dolnej granicy
        double lX = X - min;

        if ((X >= min) &amp;&amp; (X <= max)) {
            int i = (int) floor(lX / step); // obliczenie, do którego przedziału zalicza się wylosowana wartość
            histogram[i] = histogram[i] + 1; // zwiększenie licznika danego przedziału
        }
    }

    // wyprowadzenie wartości liczników na standardowe wyjście
    for (unsigned int j = 0; j < histogram.size(); j++) {
        cout << histogram[j] << endl;
    }

    return EXIT_SUCCESS;
}

Przekierowując dane ze standardowego wyjścia na plik, można zapisać otrzymane wyniki:

$ ./RandomGen > stats.txt

Teraz statystyki można wsadzić np. do OpenOffice’a i wygenerować histogramy:

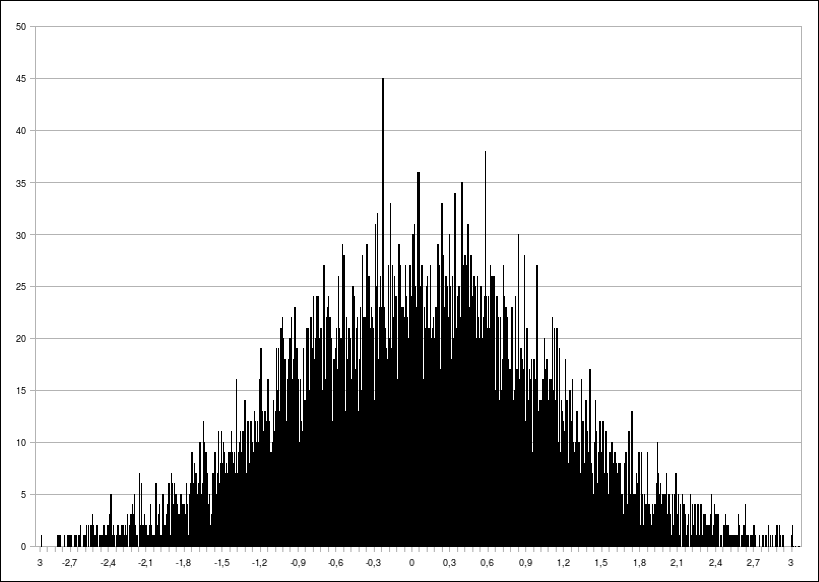
10 tys. wylosowanych liczb

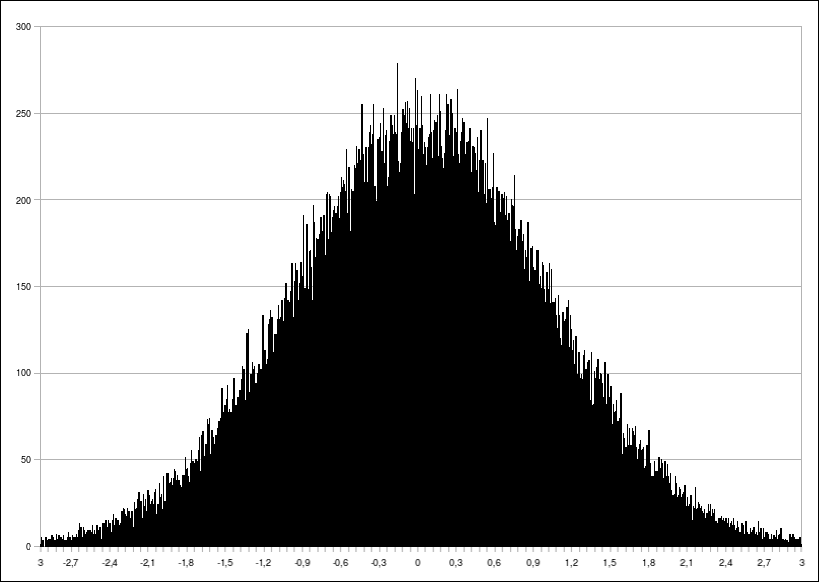
100 tys. wylosowanych liczb

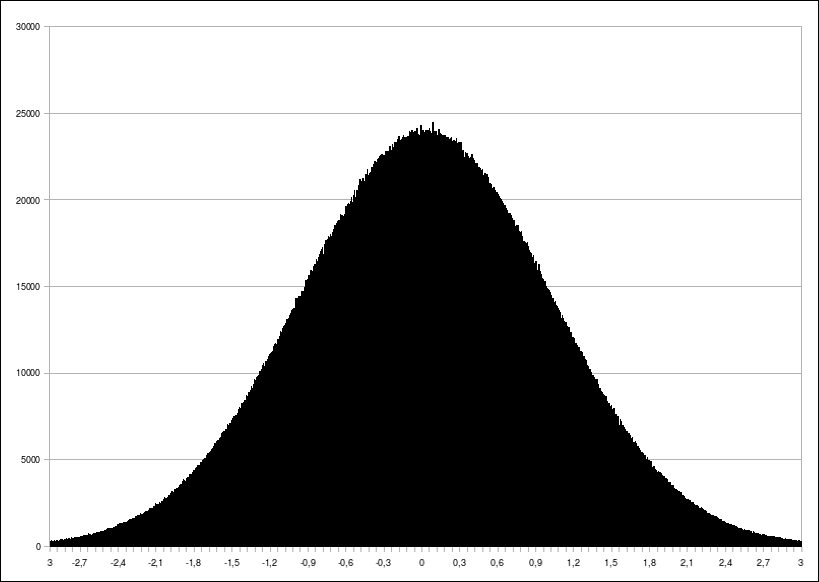
10 mln. wylosowanych liczb

Jak widzimy, im więcej wylosujemy liczb, tym histogram coraz bardziej przypomina krzywą Gaussa. Mamy więc dowód, że generator działa i otrzymujemy liczby z rozkładu normalnego. W następnym odcinku zajmiemy się rozkładem Cauchy’ego.

Podziel się: